Graph theory, a fundamental concept in mathematics and computer science, revolves around the study of graphs. These graphs are abstract representations of a set of objects where some pairs are connected by links. The foundational elements of graphs are vertices (or nodes) and edges (or links). In the realm of wireless networks, graph theory finds profound applications, offering insights and solutions to complex network challenges.
Representation of Nodes and Links: At the heart of any wireless network are devices such as routers, switches, access points, and end-user devices. These devices can seamlessly be represented as nodes (vertices) in a graph. The communication pathways or links between these devices, whether they’re Wi-Fi signals or data packet routes, manifest as edges in the graph.
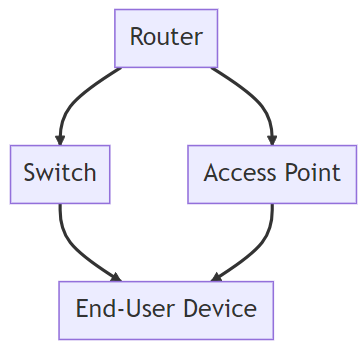
Figure 1: Nodes and Links
Dynamic Nature: One of the inherent characteristics of wireless networks is their dynamic nature. Devices frequently join or depart from the network, and the quality of communication links can fluctuate due to various factors like interference or physical obstructions. Graphs are inherently adaptable and can be updated in real-time to reflect these dynamic changes, ensuring the network’s representation remains current.
Path Analysis: The algorithms rooted in graph theory are invaluable for determining the most efficient path between two nodes. In wireless networks, this capability is paramount. It ensures data packets are routed efficiently, minimizing latency and maximizing data transfer speeds
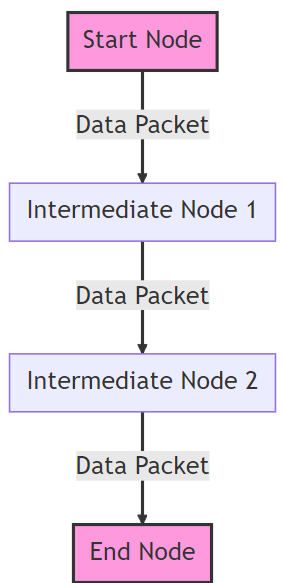
Figure 2: Path Analysis
Connectivity Analysis: Beyond just representing devices and their connections, graphs can be employed to analyze the network’s overall connectivity. They can spotlight isolated nodes or even identify critical nodes whose functionality is essential for maintaining the network’s overall connectivity.
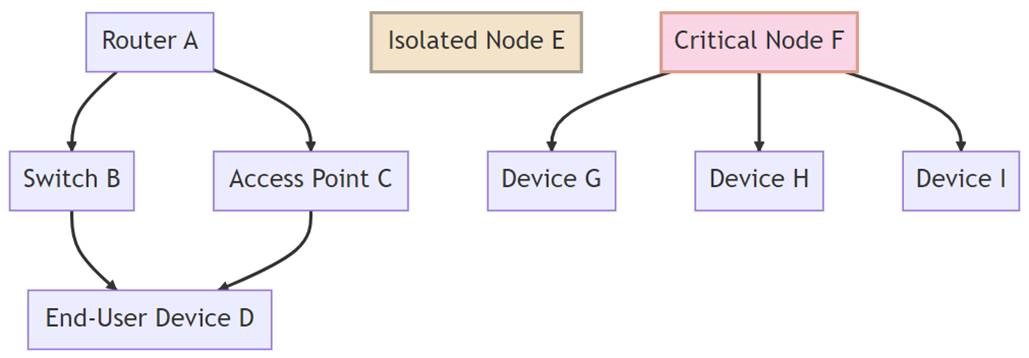
Figure 3: Connectivity Analysis
Frequency Assignment: Interference is a perennial challenge in wireless networks. To combat this, graph coloring techniques, a subset of graph theory, can be employed. These techniques can assign frequencies to transmitters in a manner that ensures adjacent transmitters don’t interfere with each other, ensuring smooth communication.
Network Resilience: How resilient is a network, especially when faced with failures? Graphs can simulate failures by removing nodes or edges, offering insights into the network’s response. Such simulations can spotlight vulnerabilities, enabling preemptive measures to bolster the network.

Figure 4: Network Resilience
Visualization: One of the most tangible benefits of using graphs is visualization. They offer a clear, visual representation of the network, simplifying it for network administrators. This visual clarity is indispensable, especially when dealing with large and intricate wireless networks where manual mapping can be both error-prone and time-consuming.
For the discovery of wireless network topologies, graph-based tools and algorithms stand out. They can autonomously detect devices within the network, ascertain their interconnections, and present a visual map of the network topology. Such automation is a boon, especially for expansive and intricate wireless networks.
In Conclusion: Graph theory is not just an abstract mathematical concept; it’s a pivotal tool in the design, analysis, and management of wireless networks. By harnessing the power of graph data structures and algorithms, network administrators are better equipped to optimize network performance, bolster security, and guarantee reliable communication, ensuring the seamless operation of our increasingly connected world.